《解三角形》大题（三）—面积问题

（一）定值

例 1：2023 年 1 月武昌区高三质量检测第 18 题

已知 $\triangle ABC$ 的内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$，已知 $3\sin C \cos A - c \cos C = -a$。

1. 求 $A$；
2. 若 $a + b = 7$，$a + c = 19$，求 $\triangle ABC$ 的面积 $S$。

例 2：2023 年 2 月深圳市高三第一次调研考试第 18 题

记 $\triangle ABC$ 的内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$，已知 $2\sin A + \frac{6bc}{a} = \pi$。

1. 求 $A$；
2. 设 $AB$ 的中点为 $D$，若 $CD = a$，且 $b - c = 1$，求 $\triangle ABC$ 的面积。

例 3：福建省部分地市 2023 届高中毕业班第一次质量检测第 18 题

记 $\triangle ABC$ 的内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$，且 $CA \cdot CB + BA \cdot BC = \frac{4}{3}c^2$，$b = 3c$，$B = 1$。

1. 求 $A$；
2. 已知 $a = 2$，求 $\triangle ABC$ 的面积。

例 4：2023 年 3 月金丽衢十二校联考第 18 题

已知 $\triangle ABC$ 中角 $A$、$B$、$C$ 对应的边分别是 $a$、$b$、$c$。已知 $(1 - \sin^2 B)(1 - \cos^2 C) = \sin^2 C \cos^2 B$，$a = 2$，$c = 2$。

1. 证明：$C = \frac{\pi}{2}$；
2. 求 $\triangle ABC$ 的面积。

例 5：2023 年 1 月桐庐中学高三第一学期期末考试第 17 题

在 $\triangle ABC$ 中，角 $A$、$B$、$C$ 所对的边分别为 $a$、$b$、$c$，且 $2\sin^2 A - 3b^2c + a^2 = 0$。

1. 求角 $A$；
2. 若 $a = 2$，$\tan A + \tan B + \tan C = 2$，求 $\triangle ABC$ 的面积。

例 6：2023 年 3 月苏锡常镇一模试卷第 18 题

在 $\triangle ABC$ 中，角 $A$、$B$、$C$ 所对的边分别为 $a$、$b$、$c$，$\sin A + 2(3\tan A + 2)\cos^2 A = 1$。

1. 若 $C = \frac{3\pi}{4}$，求 $\tan B$ 的值；
2. 若 $A = B$，$c = 2$，求 $\triangle ABC$ 的面积。

（二）取值范围

例 7：2023 年 1 月湖南雅礼中学高三月考卷（五）第 18 题

为了美化环境，某公园欲将一块空地规划建成休闲草坪，休闲草坪的形状为如图所示的四边形 $ABCD$，其中 $AB = 3$，$AD = 5$，且 $\triangle BCD$ 是以 $D$ 为直角顶点的等腰直角三角形。拟修建两条小路 $AC$，$BD$（路的宽度忽略不计），设 $\angle BAD = \theta$，$\theta \in \left(\frac{\pi}{6}, \frac{\pi}{2}\right)$。

1. 当 $\cos \theta = -\frac{5}{5}$ 时，求小路 $AC$ 的长度；
2. 当草坪 $ABCD$ 的面积最大时，求此时小路 $BD$ 的长度。

例 8：湖北省十堰市 2023 年元月高三期末调研第 18 题

在 $\triangle ABC$ 中，内角 $A$、$B$、$C$ 所对的边分别为 $a$、$b$、$c$，且 $(\sin A - \sin C)^3 - \sin B \sin C \sin B = -\sin A \sin^2 B$。

1. 求 $A$；
2. 若 $D$ 是边 $BC$ 的中点，且 $AD = 4$，求 $\triangle ABC$ 面积的最大值。

例 9：2023 年 3 月平湖市模拟考第 19 题

已知 $\triangle ABC$ 中，内角 $A$、$B$、$C$ 所对的边分别为 $a$、$b$、$c$，且满足 $\sin^2 B + \tan \frac{C}{2} = 1 + \cos^2 B - \tan \frac{B}{2}$。

1. 求角 $A$ 的大小；
2. 设 $AD$ 是 $BC$ 边上的高，且 $AD = 2$，求 $\triangle ABC$ 面积的最小值。

例 10：2023 年 2 月杭州第二中学高三下统测第 17 题

在 $\triangle ABC$ 中，内角 $A$、$B$、$C$ 所对的边分别为 $a$、$b$、$c$，且 $\cos A \sin B + \sin A \cos C = \sin B$。

1. 求 $A$；
2. 若 $AD = DC$，$BD = 3DC$，求 $\triangle ABC$ 面积的最大值。

例 11：2023 年 2 月绍兴市高三开学检测第 17 题

在 $\triangle ABC$ 中，角 $A$、$B$、$C$ 所对的边分别为 $a$、$b$、$c$，若 $a = 2$，$2\sin^3 B + 3\cos C = 3\cos B$。

1. 求角 $B$；
2. 若角 $A$ 为钝角，求 $\triangle ABC$ 面积的取值范围。

例 12：2023 年 1 月重庆缙云教育联盟高三第一次数学检测第 17 题

从秦朝统一全国币制到清朝末年，圆形方孔铜钱（简称“孔方兄”）是我国使用时间长达两千多年的货币。如图 1，这是一枚清朝同治年间的铜钱，其边框是由大小不等的两同心圆围成的，内嵌正方形孔的中心与同心圆圆心重合，正方形外部，圆框内部刻有四个字“同治重宝”。某模具厂计划仿制这样的铜钱作为纪念品，其小圆内部图纸设计如图 2 所示，小圆直径为 1，内嵌一个大正方形孔，四周是四个全等的小正方形（边长比孔的边长小），每个正方形有两个顶点在圆周上，另两个顶点在孔边上，四个小正方形内用于刻铜钱上的字。设 $\theta = \angle OAB$，五个正方形的面积和为 $S$。

1. 求面积 $S$ 关于 $\theta$ 的函数表达式；
2. 求面积 $S$ 的最小值。

例 13：2023 年 1 月中学数学小 R 三模第 18 题

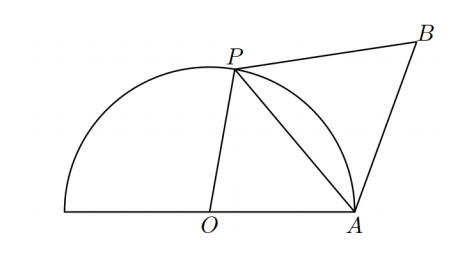
如图所示，$O$ 是半径为 2 的半圆的圆心，点 $A$ 为右端点，点 $P$ 是半圆上的一个动点，以 $PA$ 向外作一个等边三角形 $PAB$，点 $B$ 与点 $O$ 在 $PA$ 的异侧，设 $\theta = \angle POA$。

1. 若 $\theta = \frac{2\pi}{3}$，求 $PA$ 的长；
2. 求四边形 $OABP$ 面积的最大值。
   

例 14：广东河源市 2023 学年高三上学期 1 月期末第 18 题

已知锐角三角形 $ABC$ 内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$，且 $3\sin A + 2\cos A = 2 + 3\cos 2A$。

1. 求 $\sin B + \sin C$ 的取值范围；
2. 若 $a = 2\sqrt{3}$，求 $\triangle ABC$ 的面积的最大值。

例 15：2023 年 3 月湖南省湘考王第 20 题

如图，在平面四边形 $ABCD$ 中，$AB = 2$，$BC = 6$，$AD = CD = 4$。

1. 当四边形 $ABCD$ 内接于圆 $O$ 时，求角 $C$；
2. 当四边形 $ABCD$ 的面积最大时，求对角线 $BD$ 的长。
   

例 16：福建省南平市四校 2023 届高三下学期 3 月联考第 18 题

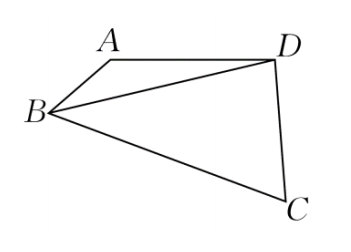
某商场计划在一个两面靠墙的角落规划一个三角形促销活动区域（即 $ABC$ 区域），地面形状如图所示。已知已有两面墙的夹角 $\angle ACB = \frac{\pi}{4}$，为锐角，假设墙 $CA$、$CB$ 的可利用长度（单位：米）足够长。

1. 在 $\triangle ABC$ 中，若 $BC$ 边上的高等于 $\frac{1}{4}BC$，求 $\sin \angle CAB$；
2. 当 $AB$ 的长度为 6 米时，求该活动区域面积的最大值。
   

例 17：2023 年 2 月湖南长郡中学高三月考（六）第 18 题

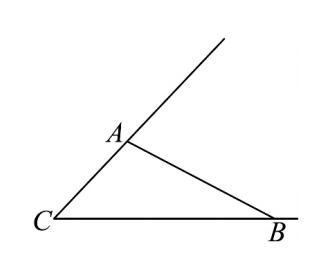
如图，在平面四边形 $ABCD$ 中，$AB = 2$，$BC = 2$，$CD = 3$，$AD = 3$。

1. 若 $DB$ 平分 $\angle ADC$，证明：$AC + \pi = 6$；
2. 记 $\triangle ABD$ 与 $\triangle BCD$ 的面积分别为 $S_1$ 和 $S_2$，求 $S_1 + S_2$ 的最大值。`

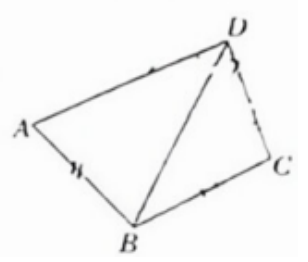
例 18：青岛市 2023 届高三下学期第二次适应性检测第 18 题

在 $\triangle ABC$ 中，角 $A$、$B$、$C$ 的对边分别是 $a$、$b$、$c$，$2\cos A \cos C = \frac{b^2 + c^2 - a^2}{2bc}$。

1. 求 $B$；
2. 若点 $D$ 为边 $BC$ 的中点，点 $E$、$F$ 分别在边 $AB$、$AC$ 上，$\angle EDF = \frac{3\pi}{2}$，$b + c = 2$。设 $\angle BDE = \alpha$，将 $\triangle DEF$ 的面积 $S$ 表示为 $\alpha$ 的函数，并求 $S$ 的取值范围。

例 19：2023 年 1 月慈溪市高三试卷第 19 题

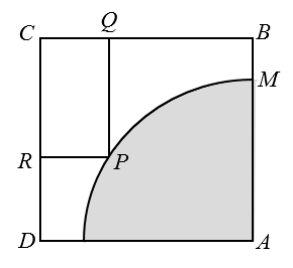
如图，$ABCD$ 是一个边长为 8m 的有部分腐蚀的正方形铁皮，其中腐蚀部分是一个半径为 6m 的扇形 $AMN$，其他部分完好可利用，铁匠师傅想在未被腐蚀部分截下一个长方形铁皮 $PRCQ$（$P$ 是圆弧上的一点），以用于制作其他物品。

1. 当长方形铁皮 $PRCQ$ 为正方形时，求此时它的面积；
2. 求长方形铁皮 $PRCQ$ 的面积 $S$ 的最大值。