《解三角形》大题（四）—外接圆与内切圆

例 1：2023 年 3 月山东聊城市高三高考模拟第 17 题

在四边形 $ABCD$ 中，$AB//CD$。

证明：$\sin \angle BAD \cdot \sin \angle BCD = \sin \angle ABC \cdot \sin \angle CDA$；
若 $AD = 1$，$AB = 3$，$BC = 3$，$\angle BAD = \angle BCD$，求 $\triangle BCD$ 外接圆的面积。

例 2：2023 年 2 月江苏省连云港市高三下学期调研第 19 题

已知 $\triangle ABC$ 的内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$，且 $2\sin C = \sin B + \cos B \tan A$。

求 $A$；
求 $\frac{\cos A}{a} + \frac{\cos C}{c} = \frac{2\sqrt{3}sinB}{\sin C} $，求 $\triangle ABC$ 外接圆的半径 $R$。

例 3：扬州市高三期初测试第 18 题

已知 $\triangle ABC$ 的内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$。$A = \frac{3\pi}{2}$，$b = 10$，$c = 6$，$\triangle ABC$ 的内切圆 $I$ 的面积为 $S$。

求 $S$ 的值；
若 $D$ 点在 $AC$ 上，且 $B$、$I$、$D$ 三点共线，求 $\overrightarrow{BD} \cdot \overrightarrow{BC}$ 的值。

例 4：杭州二中高三年级 4 月月考第 17 题

在锐角 $\triangle ABC$ 中，角 $A$、$B$、$C$ 所对的边分别为 $a$、$b$、$c$，已知 $\sqrt{3} tanA tanB = \tan A + \tan B + \tan C$。

求角 $C$ 的大小；
若 $c = 3$，求 $\triangle ABC$ 内切圆半径的取值范围。

例 5：2023 年 2 月七彩联盟返校联考第 18 题

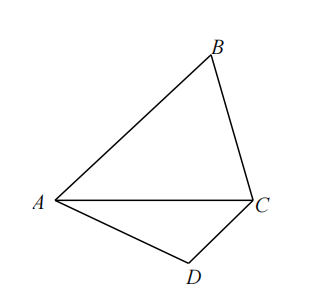
如图，平面四边形 $ABCD$ 中，$AD = 5$，$CD = 3$，$\angle ADC = 120^\circ$，$\triangle ABC$ 的内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$，且满足 $ \frac{a+b}{c}= \frac{sinA-sinC}{sinA-sinB} $。

求四边形 $ABCD$ 的外接圆半径 $R$；
求 $\triangle ABC$ 内切圆半径 $r$ 的取值范围。

例 6：2023 年 8 月河北名校高三开学考第 18 题

已知 $\triangle ABC$ 的内角 $A$、$B$、$C$ 的对边分别为 $a$、$b$、$c$，且 $b\cos C + c\cos B = \sqrt{3}\sin A$。

求 $\triangle ABC$ 外接圆的面积；
记 $\triangle ABC$ 内切圆的半径为 $r$，若 $b = \frac{\pi}{3}$，$b = 2\sqrt{3}r$，求 $\triangle ABC$ 的面积。

例 7：江苏省南通市 2023 届高三三模第 20 题

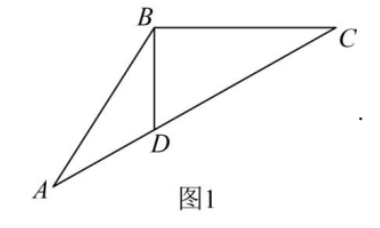
已知 $\triangle ABC$ 中，$D$ 为边 $AC$ 上一点，$AD = 1,CD = 2$。

若 $\overrightarrow{BA} \cdot \overrightarrow{BD} = \frac{3}{4}, \overrightarrow{BC} \cdot \overrightarrow{BD} = 0$，求 $\triangle ABC$ 的面积；
若直线 $BD$ 平分 $\angle ABC$，求 $\triangle ABD$ 与 $\triangle CBD$ 内切圆半径之比的取值范围。